Why do we have two completely different equations for gravitational force and two completely different equations for gravitational energy?  

.

Newton’s Universal Law of Gravitation – One set of equations for force and energy is universal and applies whenever two massive objects are interacting with each other:

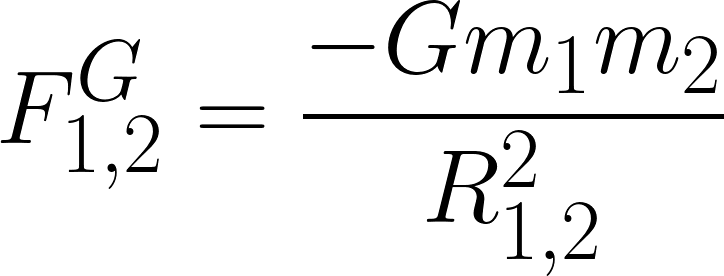
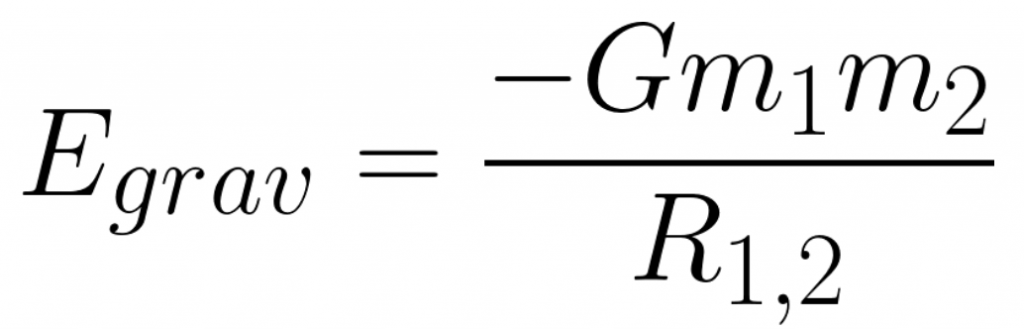
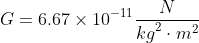
In these equations, m₁ and m₂ are the masses of the two objects and R_1,2 is the distance between their centers. Both equation have negative signs but these negative signs mean very different things. The negative sign in the gravitational force equation indicates that the gravitational force interaction is always attractive. The negative sign in the gravitational energy equation indicates that two objects have zero gravitational energy when they are infinitely far apart and their gravitational energy decreases (or becomes more and more negative) as they get closer together.

Gravitational Force and Energy Near Earth’s Surface – According to Newton’s Universal Law of Gravitation the gravitational force decreases in magnitude as object get further apart. This is certainly true but it is not very noticeable for objects near Earth surface. The gravitational force interaction between Earth and everyday objects is nearly constant as the height of the object changes. Therefore, we often make the approximation that the gravitational force does not depend on height for objects near Earth’s surface. This approximation leads to a set of equations which is very different from the universal equations above.

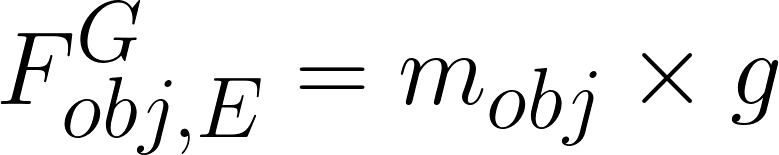
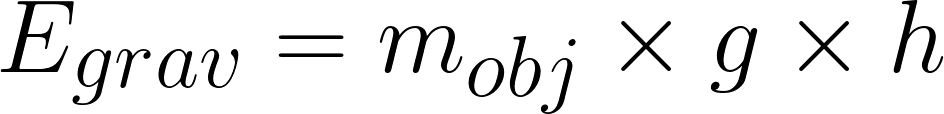
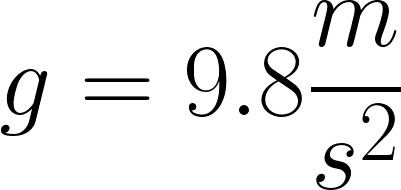
Near Earth’s surface the gravitational force does not change very much at all, so it is convenient to the approximation that the gravitational force interaction between an object and the Earth does not change with height. According to this approximation the increase in gravitational energy of the Earth-object system is directly proportional to the increase in height.

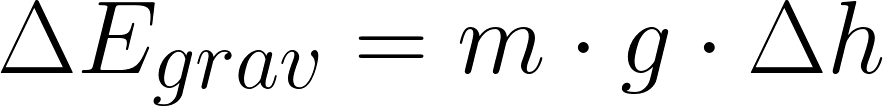
In this approximation the zero point of gravitational energy is arbitrary.